As we collaborated, Heather shared this formative assessment with me for her AP Calculus AB course. I am excited to teach this course in my face-to-face school this fall so I can definitely use it!
I try to incorporate formative assessment during all of my classes - I do a Bell Work problem every day and will often give students a "Ticket Out the Door". In an online setting, the learning objects are essential for checking student understanding. Students can take ownership of their understanding and ask their instructor specific questions regarding the topic they are working on!
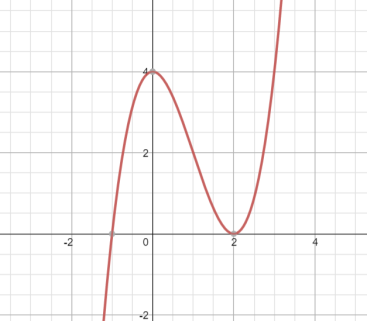
The graph of the first derivative, f’(x), on the interval [-2, 3] is provided below. Determine each of the following based on the graph.
**This post represents a collaborative effort between Alice Johnson, Heather McCormick, and Cameron Wood.
I try to incorporate formative assessment during all of my classes - I do a Bell Work problem every day and will often give students a "Ticket Out the Door". In an online setting, the learning objects are essential for checking student understanding. Students can take ownership of their understanding and ask their instructor specific questions regarding the topic they are working on!
Title of Learning Object: The graph of the derivative
Content for Learning Object (including answers):
The graph of the first derivative, f’(x), on the interval [-2, 3] is provided below. Determine each of the following based on the graph.

- State the x-values of the critical numbers for f(x).
x =-1, x = 2.
For an incorrect answer: Critical values for f(x) will appear as x-intercepts on f’(x)
- Determine if the critical values of f(x) are a relative maximum, relative minimum, or neither.
x = -1 is a relative min x=2 is neither.
For an incorrect answer: f’(x) changes from negative to positive at x=-1 so it is a relative minimum. f’(x) is positive on both sides of x=2 so it is a critical number but not an extremum.
- Determine the interval(s) where f(x) is increasing.
(-1, 2) and (2, 3)
for an incorrect answer: f’(x) is positive in the intervals (-1, 2) and (2, 3) which indicates that f(x) is increasing
- State the x-values of the inflection points for f(x).
x = 0, x = 2
For
an incorrect answer: The inflection points of f(x) are the locations of
the relative extrema for f’(x) or where the slope of the tangent line =
0.
- Determine the interval(s) where f(x) is concave down.
(0, 2)
For an incorrect answer: f’(x) is decreasing on (0, 2) which indicates that f(x) is concave down
No comments:
Post a Comment